Insert Enunciation Environment

1. What is Enunciation

Enunciation environments, available in text mode, provides environments for theorems, lemmas, corollaries, propositions, proofs, and more. One example is shown in Figure 1

2. How to insert an enunciation

Select Insert an enunciation from mode toolbar.

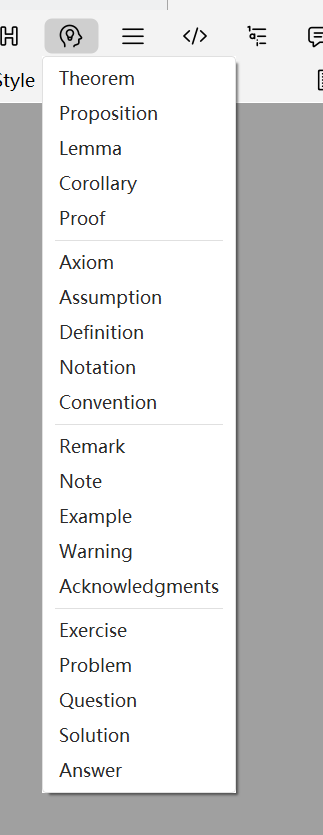
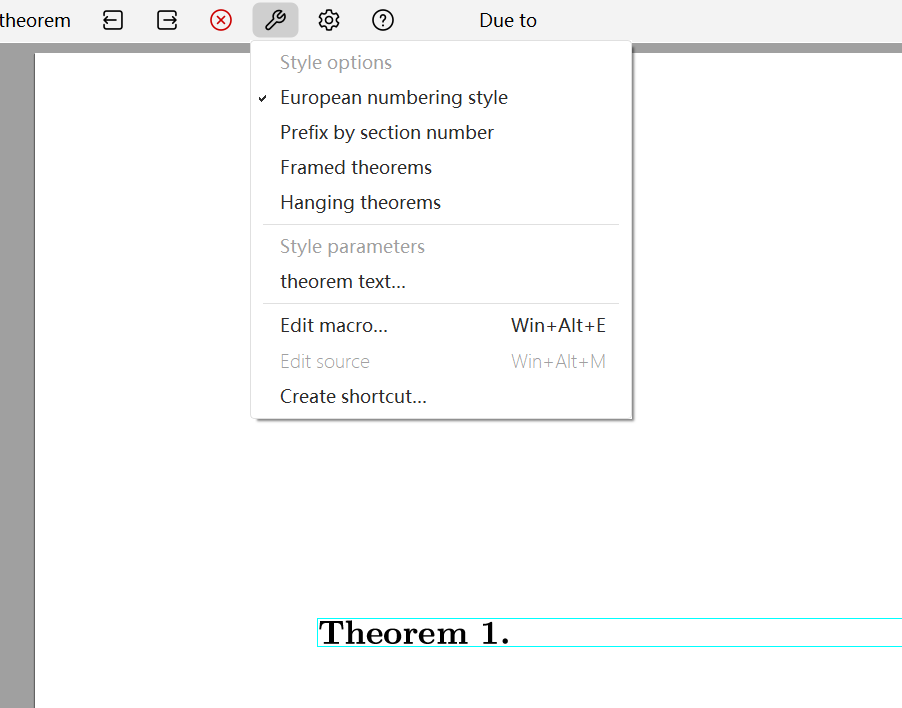
For more needs, such as numbering styles and framed theorems, please follow these steps:

1. Click the enunciation.

2. Select →Preferences for tag from Focus toolbar

3. Select the number or environment format that you need. The formatting options are explained below:

3. Enunciation Examples

a. Theorem: A core conclusion that requires rigorous proof. It represents a primary contribution to the work.

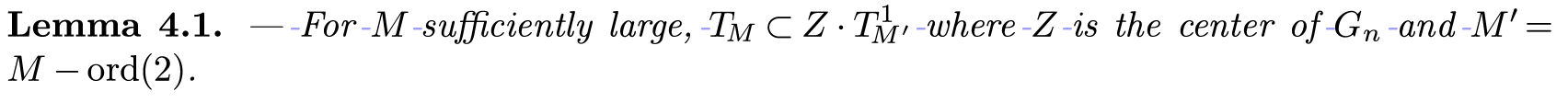
b. Lemma: An auxiliary conclusion that provides an intermediate step for proving a theorem or proposition.

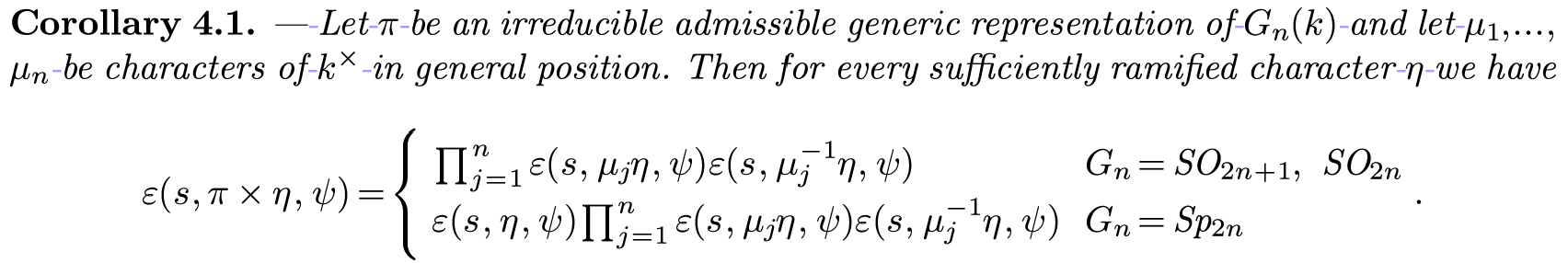
c. Corollary: A direct extension derived from a theorem or proposition, requiring brief supplementary proof.

d. Proposition: An independent statement, often considered a minor theorem or an unnamed theorem.

e. Proof: The process of logical deduction that verifies the validity of a theorem, lemma, proposition, or corollary.

Liii STEM provides a wide range of enunciation types. As listed below:

Classification	Enunciation
Mathematical Theorems	Theorem, Lemma, Corollary, Proposition, Axiom, Assumption.
Definitions & Explanations	Definition, Notation, Convention.
Remarks & Notes	Remark, Note, Warning.
Examples & Exercises	Example, Exercise, Problem, Question, Solution, Answer.
Other	TypesProof, Acknowledgments.
...

4. Recommendations for Using Enunciations

Note that the appearance of the same enunciation differs depending on the language style. For example, content within a Theorem is displayed in upright Roman in Chinese styles, but in italics in English styles.

Avoid nesting enunciations.